本文基于 Cyfrin Updraft 的 Uniswap V3 课程整理,深入探讨 V3 的核心创新。
前言
Uniswap V3 是 DeFi 历史上最重要的创新之一,它通过引入集中流动性(Concentrated Liquidity)机制,将资金效率提升了 4-200 倍,彻底改变了 AMM 的游戏规则。
但 V3 也因此变得复杂:从简单的 到复杂的 Tick 机制,从 ERC20 的 LP Token 到 ERC721 的 NFT 仓位,从被动做市到主动管理。
通过本文,你将:
- 理解 V3 为什么需要存在:V2 的根本问题是什么?
- 掌握集中流动性的核心思想:如何用更少的资金提供更深的流动性?
- 理解 V2 与 V3 的架构差异:从储备量到价格的设计转变
- 掌握 Tick 机制:为什么用离散的整数表示价格?
- 掌握储备量计算公式:给定 L 和价格区间,如何计算 x 和 y?
- 了解合约架构:V3 的合约体系是如何组织的?
从 V2 到 V3
V2 的工作原理
在深入 V3 之前,我们先简单回顾 Uniswap V2 的核心机制。
恒定乘积公式:
其中:
- = token0 的储备量
- = token1 的储备量
- = 常数(也可表示为 ,其中 是流动性)
价格由储备量决定:
例如,如果池子里有 100 ETH 和 180,000 USDC,那么价格为 USDC/ETH。
流动性均匀分布:这是 V2 的关键特性,流动性均匀分布在 0 到 ∞ 的整个价格区间,无论价格是 0.01 还是 10,000,池子都需要持有两种代币的组合。
V2: 资金利用率极低
V2 存在一个致命问题:大部分流动性永远不会被使用。
案例:DAI/USDC 稳定币对
这两个都是美元稳定币,价格理论上维持在 1:1 附近,实际上绝大多数时候价格都在 0.99 到 1.01 之间波动。
但在 V2 中,你的流动性分布在哪里?答案是:0 到 ∞ 的整个价格区间!
这意味着:
- 你的大部分资金分布在 0.5、0.8、1.5、10、100 等永远不会触及的价格
- 真正在 0.99-1.01 区间工作的资金只是很小一部分
- 剩下的资金都在"空转",不产生任何手续费收益
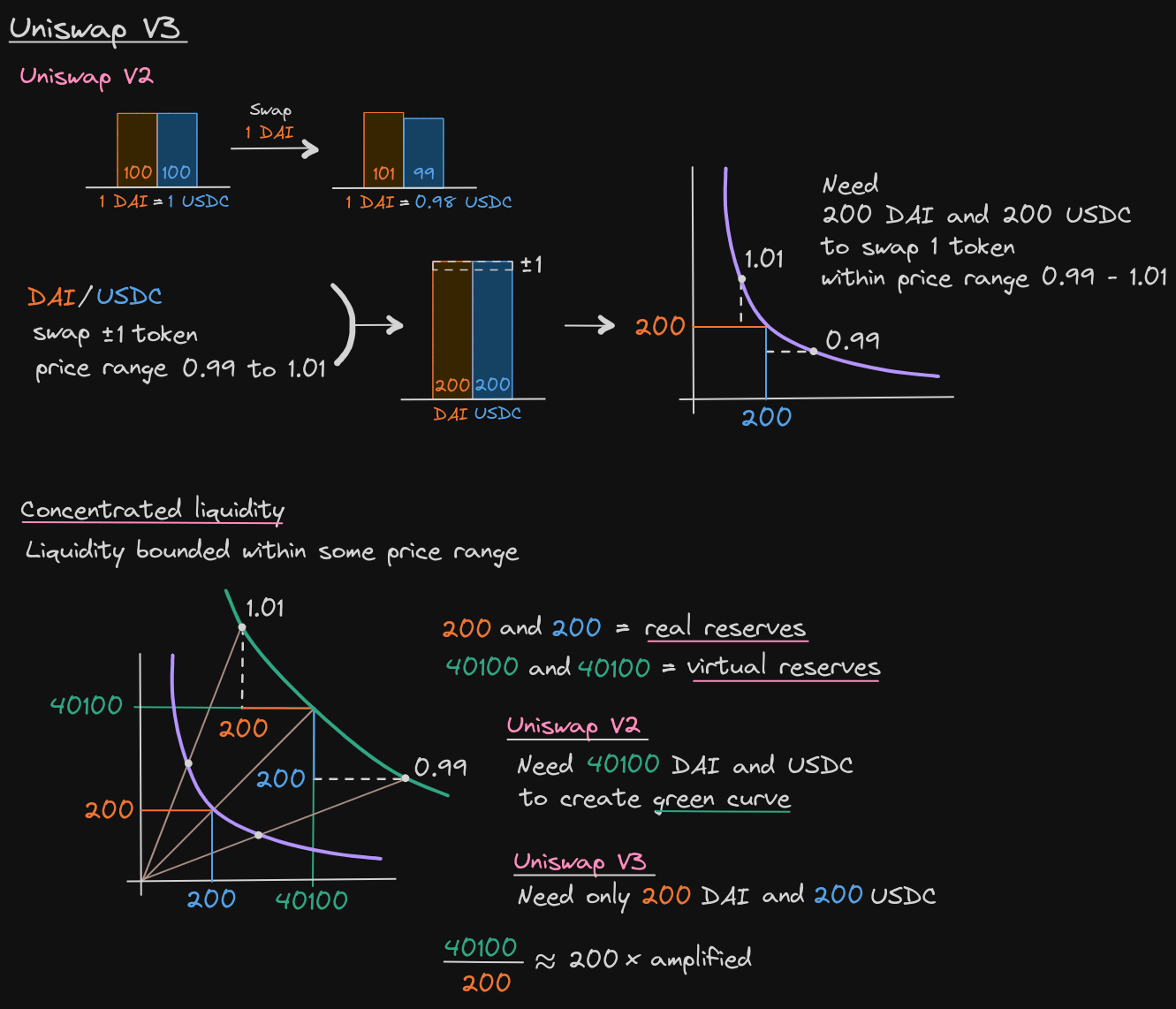
数据对比:
- V2:要在 0.99-1.01 价格区间内提供足够的流动性深度,需要约 40,100 DAI + 40,100 USDC
- V3:只需要 200 DAI + 200 USDC 就能达到相同效果
- 资金效率提升: 倍
V3: 集中流动性
Uniswap V3 提出了革命性的解决方案:让 LP 自己决定将流动性集中在哪个价格区间。
核心思想:
传统 V2 的问题是流动性被强制均匀分布在 0 到 ∞。V3 的解决方案是允许 LP 说:"我只想在 0.99 到 1.01 这个价格区间提供流动性"。
这样,同样的 200 DAI + 200 USDC,在 V3 中可以:
- 只在 0.99-1.01 区间激活
- 在这个区间内提供与 40,100 DAI + 40,100 USDC 等价的流动性深度
- 价格移出区间后,流动性变为单一代币,停止工作
虚拟储备量与真实储备量:
V3 引入了两个重要概念:
- 真实储备量(Real Reserves):LP 实际存入合约的代币数量,例如 200 DAI 和 200 USDC
- 虚拟储备量(Virtual Reserves):在价格区间内等价的"完整曲线"的储备量,例如 40,100 DAI 和 40,100 USDC
在 V2 中,真实储备量 = 虚拟储备量。在 V3 中,真实储备量 << 虚拟储备量(在集中的价格区间内)。
不同资产的效率提升:
资金效率提升的倍数取决于你设置的价格区间宽度:
| 资产类型 | 价格区间 | 效率提升 |
|---|---|---|
| 稳定币对(DAI/USDC) | 0.99 - 1.01 | 200x |
| 稳定币对 | 0.95 - 1.05 | 50x |
| 相关资产(ETH/stETH) | ±10% | 10-20x |
| 波动资产(ETH/USDC) | ±50% | 4-8x |
| 波动资产 | 全价格区间 | 1x(等同 V2) |
价格区间越窄,资金效率提升越高。但风险是:价格移出区间后,你就不再赚取手续费了。
设计架构
V2 和 V3 最大的区别不是手续费多少,也不是 LP Token 的形式,而是它们对"流动性池"这个概念的理解方式完全不同。
V2 从储备量到价格
核心思路:存储代币储备量,根据储备量计算一切。
追踪的状态变量:
uint112 private reserve0; // token0 的储备量 uint112 private reserve1; // token1 的储备量
计算方向:储备量 → 流动性 和价格
公式体系:
特点:
- 简单直接:储备量就是真实持有的代币数
- 被动管理:LP 无法选择价格区间
- 单一手续费档位:0.3% 固定费率
- ERC20 LP Token:可互换的流动性凭证

V3 从价格到储备量
核心思路:存储价格和流动性,根据它们计算储备量。
追踪的状态变量:
uint160 public sqrtPriceX96; // 当前价格(√P * 2^96) uint128 public liquidity; // 当前激活的流动性 mapping(int24 => Tick) public ticks; // 每个 tick 的流动性数据
计算方向:流动性 和价格区间 → 储备量
公式体系(不懂没关系,留个印象,下面再讲):
特点:
- 复杂但灵活:支持多个价格区间的流动性叠加
- 主动管理:LP 自定义价格区间
- 多档手续费:0.01%, 0.05%, 0.3%, 1%
- ERC721 NFT:每个仓位是独特的 NFT

这个设计转变的核心原因是:为了支持集中流动性。
在 V2 中,如果你存储储备量,那么所有 LP 的流动性必须在同一条曲线上(因为储备量是全局唯一的)。
在 V3 中,通过存储价格和"每个价格区间的流动性",可以让不同 LP 在不同价格区间提供流动性,这些流动性可以灵活叠加。
举例:
- LP Alice 在 [1500, 2000] 提供流动性
- LP Bob 在 [1700, 1900] 提供流动性
- 当价格在 1700-1900 时,总流动性 =
- 当价格在 1500-1700 时,总流动性 =
这种灵活性在 V2 的架构下无法实现。
V3 虚拟储备量
在一条恒定乘积曲线上,任意一点 满足 。
在 V3 中,我们构造一条局部等价的曲线:
- 在价格区间 内,这条曲线的形状与原曲线完全一致
- 但这条曲线不经过原点,从而减少所需的真实储备量

虚拟储备量的定义:
给定一个价格区间 和当前价格 (在区间内),我们定义:
其中:
- = 真实储备量(实际持有的代币)
- = 虚拟储备量(使曲线"完整"所需的额外代币)
- = 流动性
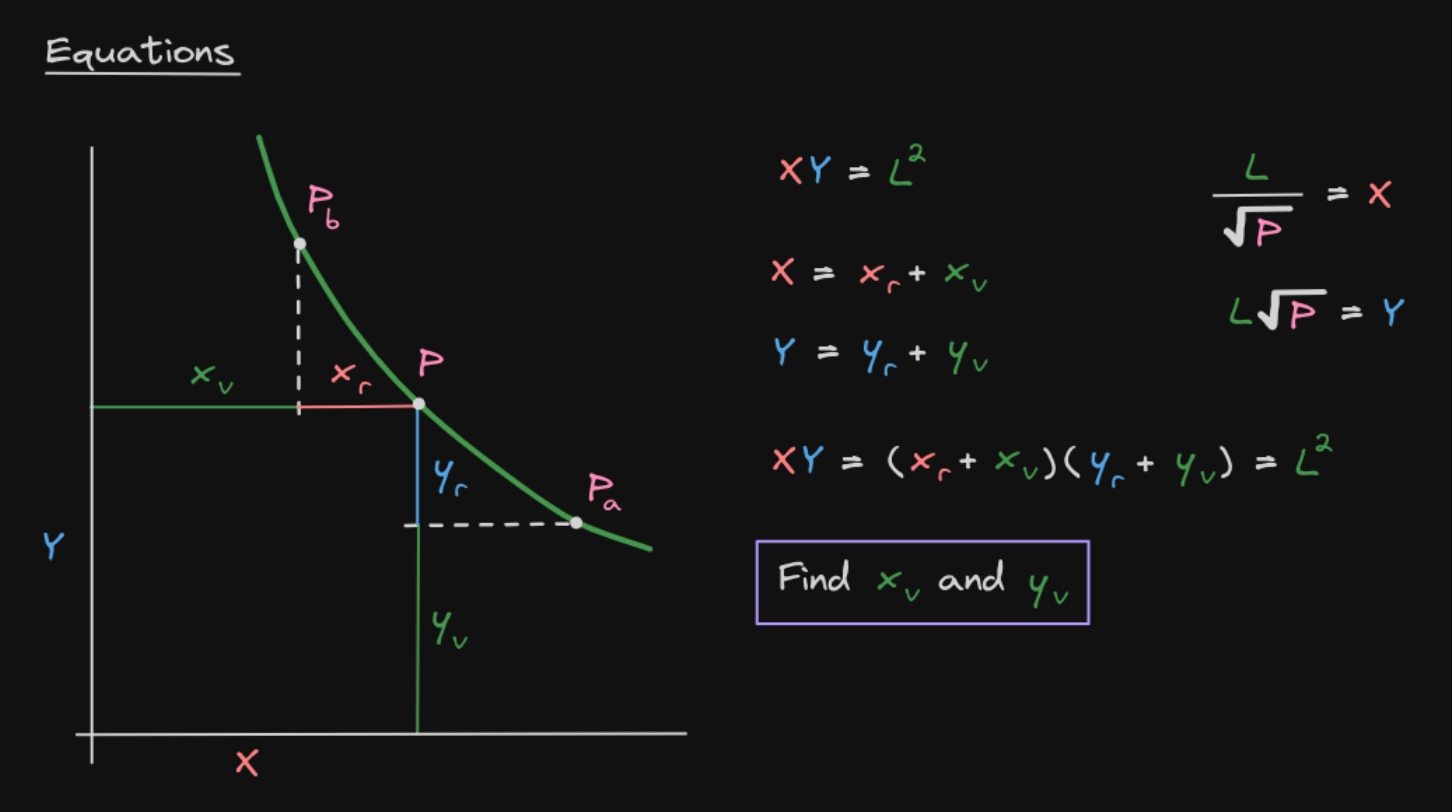
虚拟储备量的计算:
当价格在 时:
- 从 到 (价格上升), 逐渐减少到 0:
所以 减少了:
这就是真实持有的 数量!
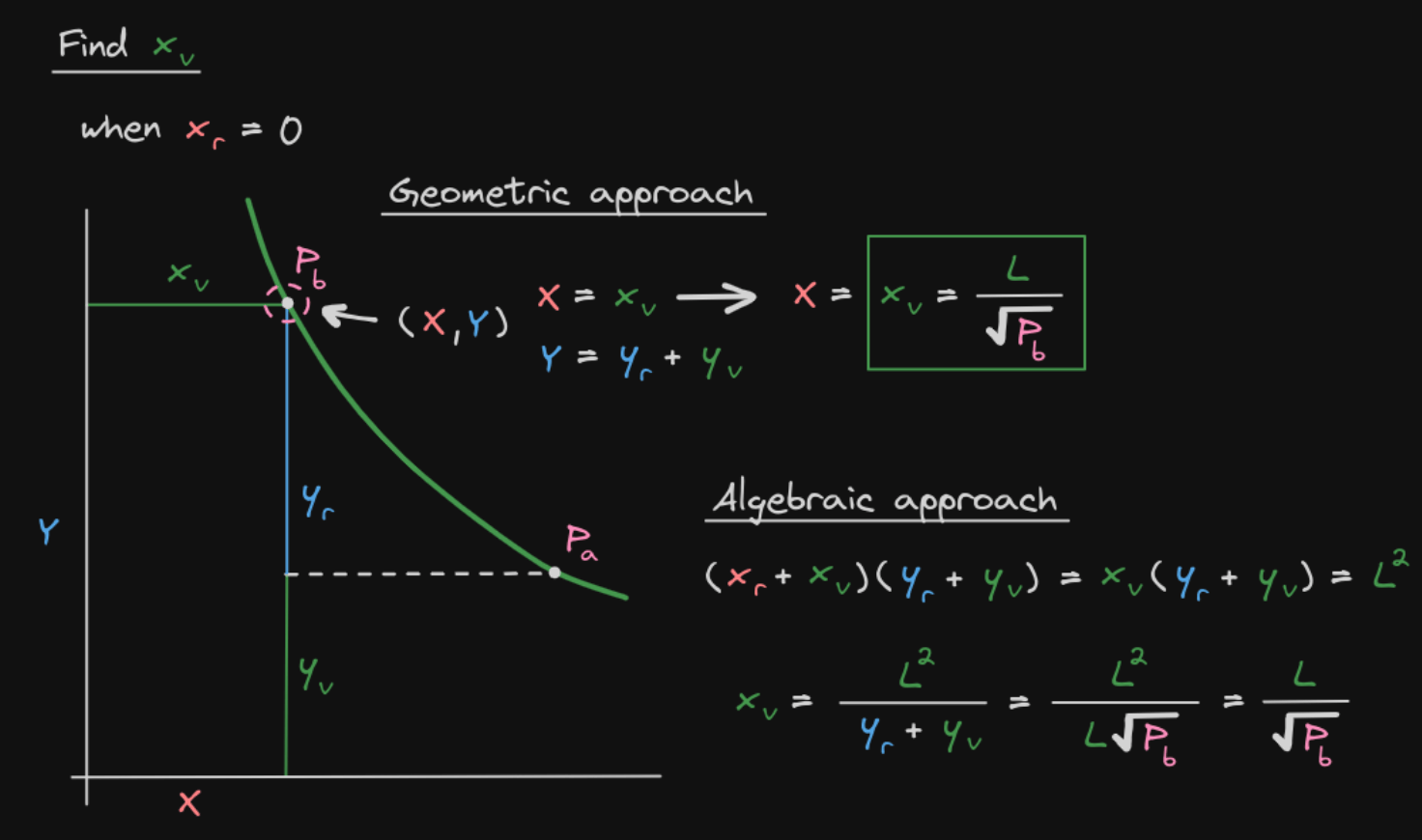
- 从 到 (价格上升), 逐渐增加:
所以 增加了:
这就是真实持有的 数量!
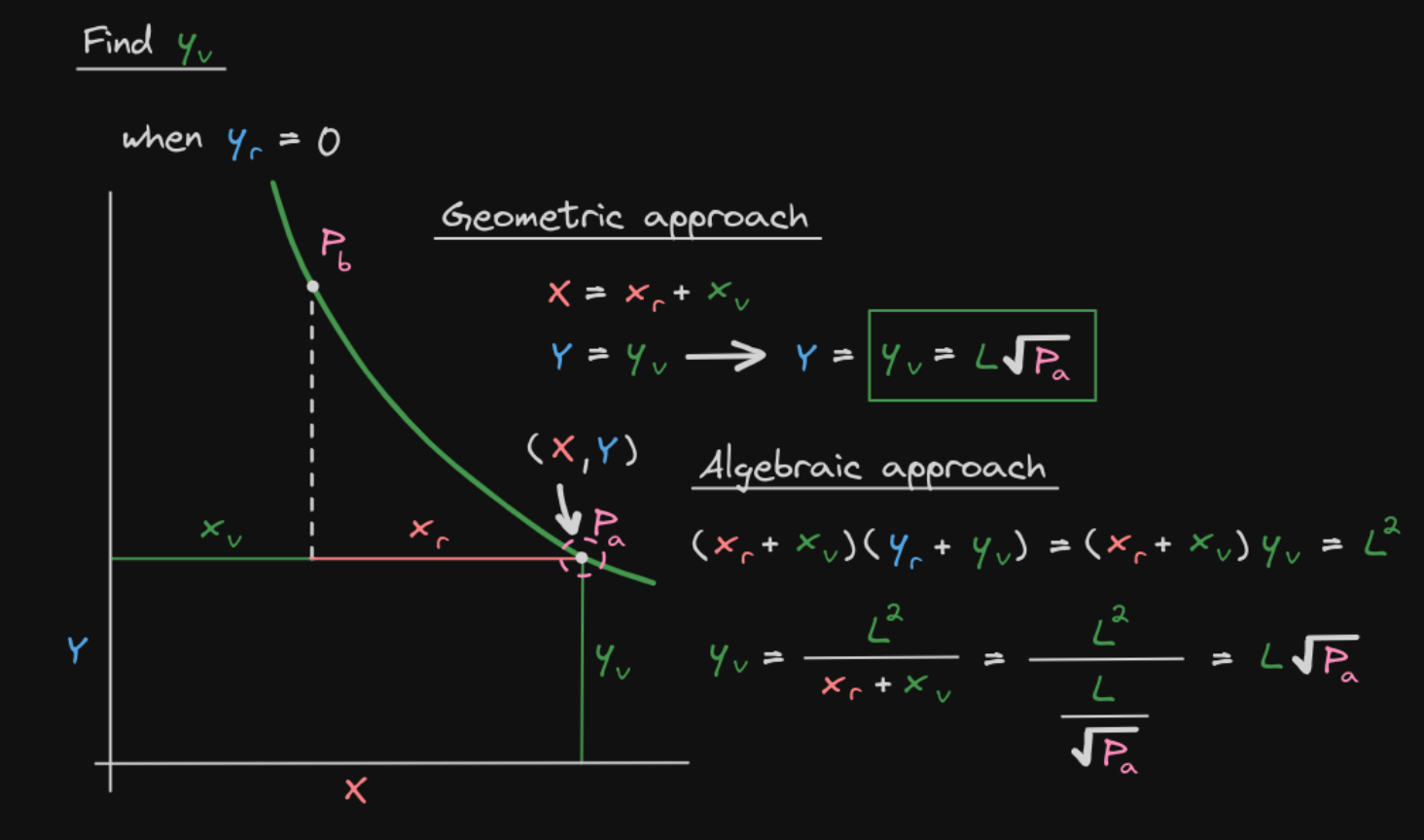
验证:
这正好是在价格 点的完整曲线坐标!
V3 的优缺点
优点
1. 资金效率大幅提升
- 稳定币交易对:100-200 倍
- 相关资产:10-20 倍
- 波动资产:4-8 倍
2. 单边流动性(Range Limit Order)
V3 支持只提供一种代币的流动性。将价格区间设置在当前价格的上方或下方,相当于一个去中心化的限价单,而且在价格上涨过程中还赚取手续费。
3. 多档手续费设计
| 手续费 | 适用场景 | Tick Spacing |
|---|---|---|
| 0.01% | 稳定币对(DAI/USDC) | 1 |
| 0.05% | 相关资产(ETH/stETH) | 10 |
| 0.3% | 标准交易对(ETH/USDC) | 60 |
| 1% | 异常波动资产 | 200 |
缺点
1. 需要主动管理流动性
价格移出你设置的区间后,你就不再赚取手续费。需要:
- 监控价格:定期检查价格是否在你的区间内
- 重新平衡:价格移出后,重新设置价格区间
- 策略调整:根据市场波动调整区间宽度
2. 非同质化 Token(ERC721)
每个流动性仓位是一个独特的 ERC721 NFT,因为不同仓位的价格区间、流动性数量、手续费累积都不同。
影响:
- 不能直接交易 LP 仓位(在 v2 里,LP Token 是 ERC20,可以直接交易)
- 不能直接用作抵押品
- 不能简单地组合和拆分(每个 NFT 代表特定参数的仓位,合并需要重新创建新仓位)
3. 更高的 Gas 成本
V3 的操作比 V2 更复杂,Gas 成本通常是 V2 的 1.5-2 倍。
Tick 机制
V3 需要支持多个价格区间的流动性叠加,这带来了几个技术挑战:
挑战 1:如何追踪多个价格区间?
当价格在 1700-1900 时,总流动性 = 。但价格是连续的,我们不可能为每一个可能的价格都存储一个流动性值!
挑战 2:如何快速查找"下一个激活的价格区间"?
在交换过程中,价格可能从 1850 变化到 1920,跨越了多个价格区间。我们需要高效地找到这些"边界价格"。
挑战 3:如何在链上节省存储和计算成本?
Solidity 不支持浮点数,我们需要用整数表示价格。而且,存储和计算的成本必须尽可能低。
Tick 的解决方案:
Uniswap V3 通过 Tick 机制 解决了这些问题:
- 离散化价格空间:将连续的价格空间分割成离散的"刻度"(tick)
- 用整数表示价格:每个 tick 是一个整数,对应一个特定的价格
- 只存储有流动性的 tick:大幅节省存储空间
- 高效查找边界:通过数据结构(Tick Bitmap)快速找到下一个激活的 tick
简单来说:Tick 是价格的离散化索引。
数学定义
基础公式
V3 使用一个优雅的指数函数来建立 tick 和价格的关系:
其中:
- = 价格(token1 / token0,即 的比例)
- = 整数,表示价格的"刻度"
Tick 的范围
V3 限制了 tick 的范围:
这对应的价格范围是:
这个范围足够覆盖现实中所有可能的资产价格。
关键特性
1. tick = 0 时,
2. 每增加 1 个 tick,价格变化 0.01%
所以,相邻两个 tick 之间的价格变化是 0.01%。
3. 为什么选择 1.0001?
这是一个精度和范围的权衡:
| 基数 | 每 tick 价格变化 | 达到 2倍价格需要的 tick 数 | 评价 |
|---|---|---|---|
| 1.001 | 0.1% | ~693 | 粒度太粗,不够精细 |
| 1.0001 | 0.01% | ~6931 | ✓ 平衡点 |
| 1.00001 | 0.001% | ~69314 | 粒度太细,浪费空间 |
1.0001 提供了足够的精度(0.01% 对大多数交易对够用)、合理的范围,以及良好的计算效率。
sqrtPriceX96
在实际合约中,V3 不是直接存储 tick 或 Price,而是存储一个叫 sqrtPriceX96 的值。
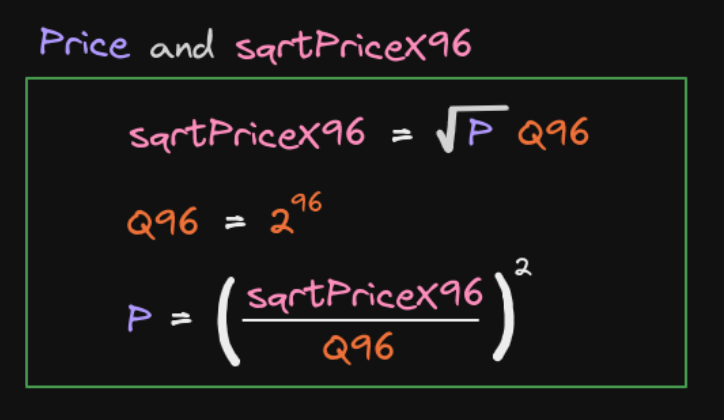
优化 1:为什么用 √P(平方根价格)?
回顾恒定乘积公式 ,如果我们用 改写,得到:
类似地:
可以看到, 是储备量公式的自然形式。
使用 的好处:
- 公式更简洁:,
- 避免开方运算:在合约中,如果存储 ,计算 和 时只需要一次乘法或除法
- 数值稳定性: 的变化范围比 小,数值计算更稳定
优化 2:为什么用 X96(定点数)?
Solidity 不支持浮点数,所有数字都是整数。但 通常是一个小数,怎么用整数表示?
答案是:定点数(Fixed-Point Arithmetic)。
V3 选择了 Q64.96 格式:
- Q 表示 "Q format"(定点数格式)
- 64 表示整数部分有 64 位
- 96 表示小数部分有 96 位
所以:
这个数是一个 uint160(160 位无符号整数)。
举例说明
案例:ETH/USDC,价格 USDC/ETH
- 计算 :
- 计算 sqrtPriceX96:
- 在合约中存储:
uint160 sqrtPriceX96 = 3543191142285914205922034791424;
反向转换
从 sqrtPriceX96 恢复价格:
// sqrtPriceX96 -> P(更精确的计算) uint256 price = (uint256(sqrtPriceX96) * uint256(sqrtPriceX96) * 1e18) >> (96 * 2);
Tick 与 sqrtPriceX96 的关系

从 tick 计算 sqrtPriceX96
由公式 ,得到:
在合约中的实现使用了高效的算法,避免了直接计算指数,而是通过:
- 二进制分解:将 tick 分解为 2 的幂次和
- 查表法:预计算一些关键值
- 位运算:用移位代替乘除法
从 sqrtPriceX96 计算 tick
反向计算需要用到对数:
由于 ,我们有:
Tick Spacing
虽然理论上相邻 tick 之间差 1(价格变化 0.01%),但 V3 引入了 Tick Spacing 的概念。
定义:Tick Spacing 是允许使用的 tick 的最小间隔。
例如,如果 tickSpacing = 60,那么只有以下 tick 可以使用:
..., -120, -60, 0, 60, 120, 180, ...
为什么需要 Tick Spacing?
原因 1:减少存储开销
如果每个 tick 都可以使用,那么池子可能有成千上万个活跃的 tick 需要存储。通过 tickSpacing,可以将活跃 tick 的数量减少到原来的 1/tickSpacing。
原因 2:匹配手续费档位
不同波动性的资产,需要不同的价格粒度:
| 手续费 | Tick Spacing | 价格粒度 | 适用场景 |
|---|---|---|---|
| 0.01% | 1 | 0.01% | 稳定币对 |
| 0.05% | 10 | 0.1% | 相关资产 |
| 0.3% | 60 | 0.6% | 标准资产 |
| 1% | 200 | 2% | 高波动资产 |
计算储备量
现在我们已经理解了 Tick 和 sqrtPriceX96,是时候解决 V3 的核心数学问题了:
给定流动性 和价格区间 ,如何计算需要的代币数量 和 ?
这是 V3 架构转变(从储备量到价格)的数学基础,也是所有后续操作的根基。
基础公式(单点价格)
从最基本的恒定乘积公式出发,推导出 和 的表达式。
恒定乘积公式:
在一条恒定乘积曲线上,任意点 满足:
其中 是流动性(常数)。同时,价格定义为:
推导 x 的公式:
从两个公式出发:
从 (2) 得到:
代入 (1):
关键公式 1:
推导 y 的公式:
从 和 :
关键公式 2:
小结:
这两个公式的对称性非常优美:
这意味着:
- 当价格 上升(资产变贵)时: 的数量减少(稀缺资产变少), 的数量增加(报价资产变多)
- 当价格 下降(资产变便宜)时: 的数量增加, 的数量减少
价格区间内的储备量
现在让我们将这些公式扩展到价格区间。
问题设定:
给定:
- 流动性 (常数)
- 价格区间 ,其中
- 当前价格 (可能在区间内,也可能在区间外)
求:LP 需要持有多少 和 ?
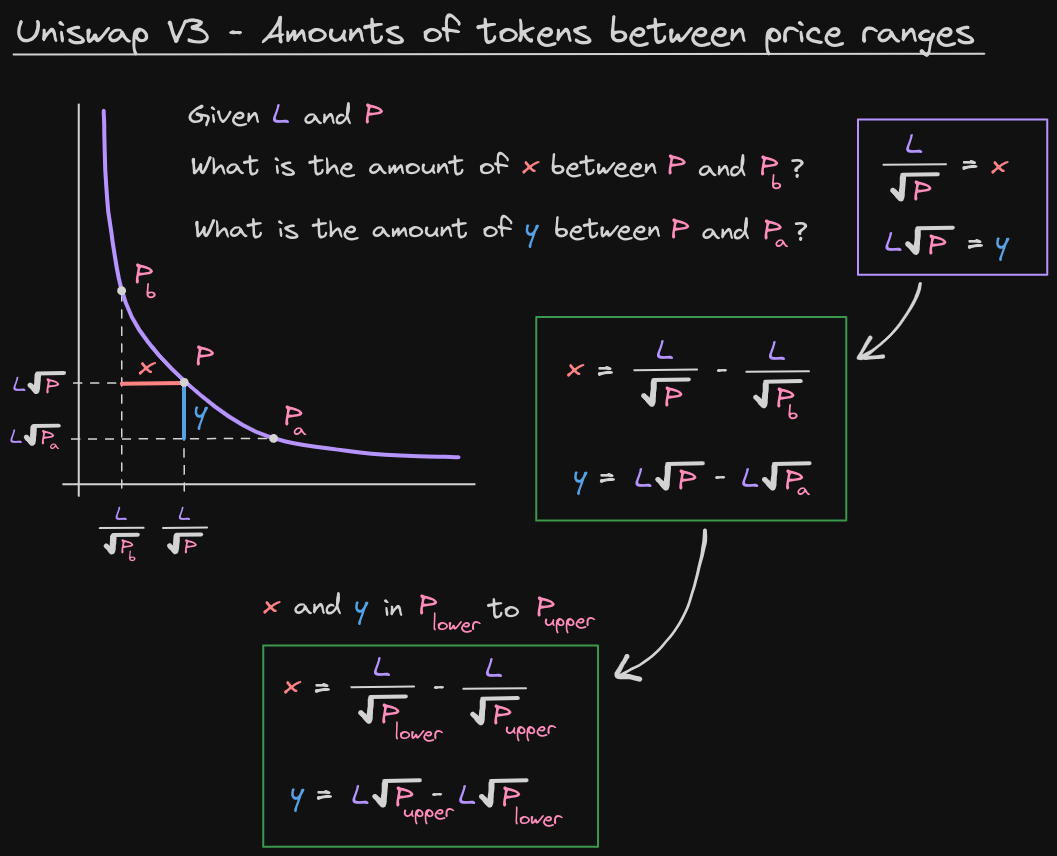
几何理解:
在恒定乘积曲线上:
- 的数量:从 到 的距离
- 的数量:从 到 的距离
推导 x 的公式:
当价格从 变化到 时:
在 点:
在 点:
的变化量(也就是 LP 实际持有的 ):
推导 y 的公式:
当价格从 变化到 时:
在 点:
在 点:
的变化量(也就是 LP 实际持有的 ):
通用公式总结:
对于价格区间 ,当前价格 :
三种特殊情况
在实际应用中,当前价格 相对于价格区间 有三种可能的位置关系。
情况 1:价格在区间内()
这是最常见的情况,LP 同时持有两种代币:
价格在区间上方()
当价格高于区间上界时,LP 的所有代币都被换成了 (token1):
实际意义:价格上涨,ETH 全部被卖出换成了 USDC,LP 不再提供流动性,相当于一个"自动止盈"。
价格在区间下方()
当价格低于区间下界时,LP 的所有代币都被换成了 (token0):
实际意义:价格下跌,USDC 全部被用来买入 ETH,LP 不再提供流动性,相当于一个"自动抄底"。
流动性的计算
在实际使用中,LP 通常是这样操作的:
- 我想在价格区间 [, ] 添加流动性
- 我有 数量的 token0 和 数量的 token1
- 问:我应该添加多少流动性 ?
从 Δx 计算 L:
从公式 ,提取 :
从 Δy 计算 L:
从公式 ,提取 :
实际添加流动性的逻辑:
当用户添加流动性时,通常会指定 amount0Desired 和 amount1Desired。但由于价格比例的限制,可能无法完全使用这两个数量。
合约的处理逻辑:
// 1. 分别计算两种代币对应的 L uint128 liquidity0 = getLiquidityForAmount0( sqrtPriceX96, sqrtPriceUpperX96, amount0Desired ); uint128 liquidity1 = getLiquidityForAmount1( sqrtPriceLowerX96, sqrtPriceX96, amount1Desired ); // 2. 取较小值(确保两种代币都足够) uint128 liquidity = liquidity0 < liquidity1 ? liquidity0 : liquidity1; // 3. 计算实际需要的代币数量 uint256 amount0 = getAmount0ForLiquidity(..., liquidity); uint256 amount1 = getAmount1ForLiquidity(..., liquidity);
为什么取较小值?
因为如果取较大值,可能导致某种代币不够。所以取较小值,确保两种代币都足够,剩余的退还给用户。
价格变化时的代币数量变化
添加 Δx 后价格如何变化?
假设当前价格在区间内,现在向池子添加 数量的 token0(买入 token1)。
从 解出新价格:
或者,用 sqrtPrice 表示:
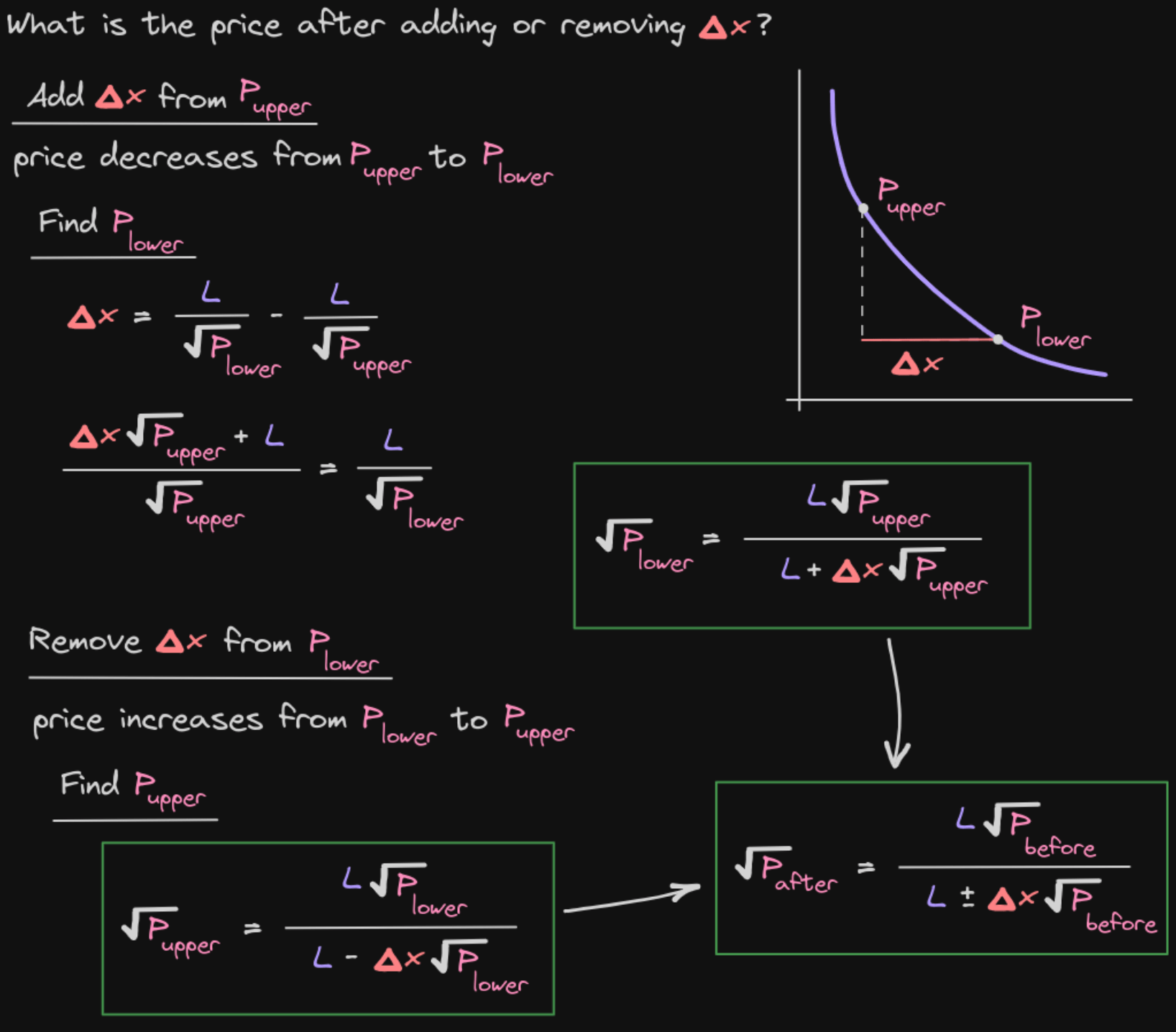
添加 Δy 后价格如何变化?
从 解出新价格:
或者:
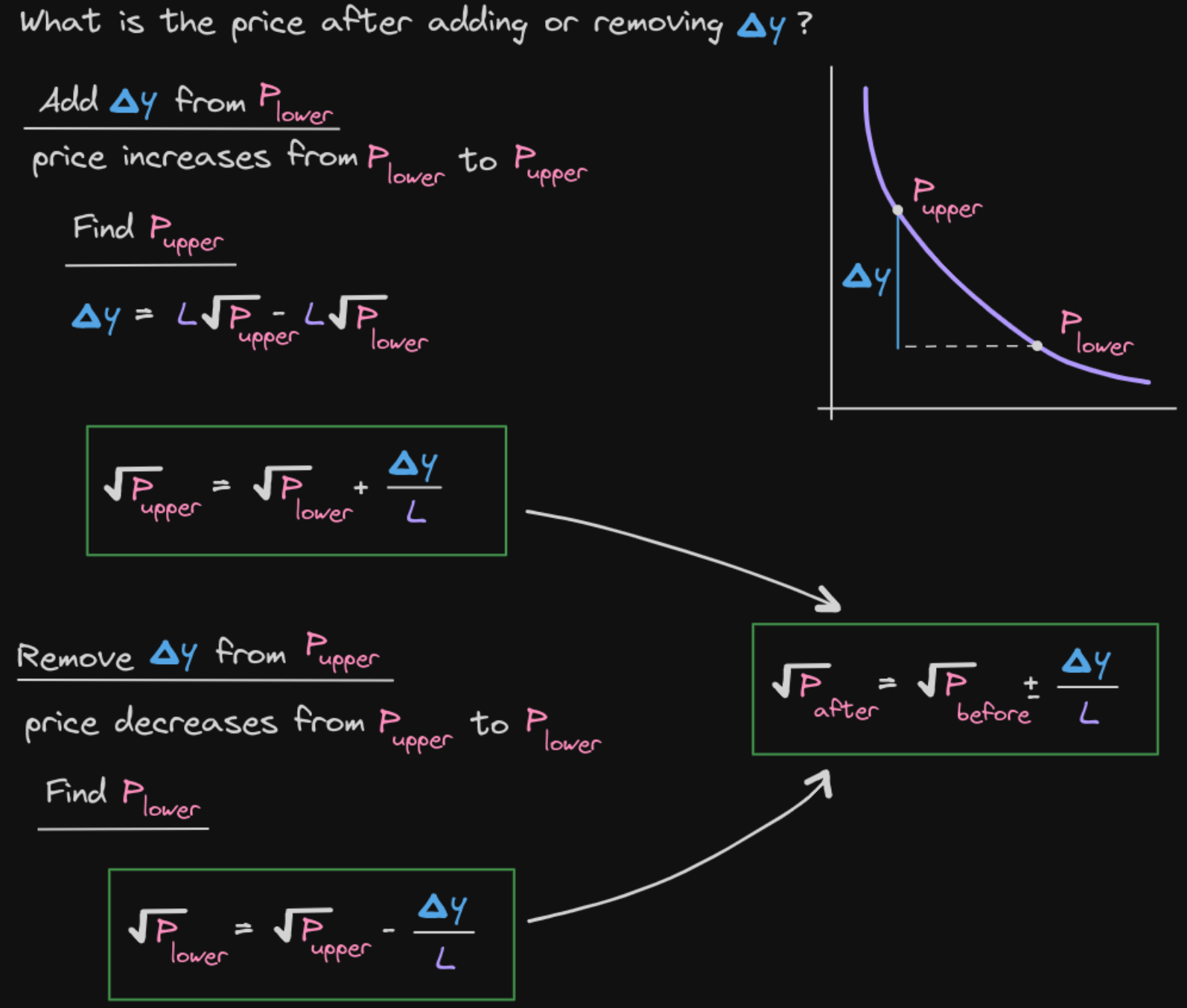
公式对比:
| 操作 | 价格变化公式 | 特点 |
|---|---|---|
| 添加 | 非线性(分式) | |
| 添加 | 线性 |
这个不对称性是 V3 数学的一个有趣特性。
合约架构概览
在深入理解了 V3 的数学原理后,让我们看看这些机制如何在智能合约中实现。
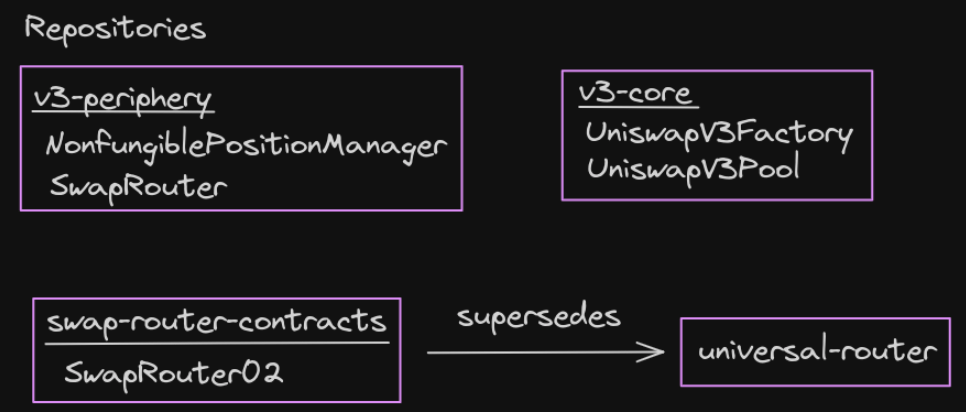
合约体系结构
Uniswap V3 的合约分为两个主要仓库:
v3-core(核心合约)
UniswapV3Factory.sol
contract UniswapV3Factory { // 创建新的交易对池子 function createPool( address tokenA, address tokenB, uint24 fee // 手续费档位:500(0.05%), 3000(0.3%), 10000(1%) ) external returns (address pool); // 查询池子地址 function getPool( address tokenA, address tokenB, uint24 fee ) external view returns (address pool); }
UniswapV3Pool.sol(最核心的合约)
contract UniswapV3Pool { // 核心状态变量 struct Slot0 { uint160 sqrtPriceX96; // 当前价格 int24 tick; // 当前 tick uint16 observationIndex; // TWAP 索引 // ... 其他字段 } Slot0 public slot0; uint128 public liquidity; // 当前激活的流动性 mapping(int24 => Tick.Info) public ticks; // tick 数据 mapping(bytes32 => Position.Info) public positions; // 仓位数据 // 核心函数 function swap(...) external returns (int256, int256); function mint(...) external returns (uint256, uint256); function burn(...) external returns (uint256, uint256); function collect(...) external returns (uint128, uint128); function flash(...) external; }
关键数据结构:
// Tick 信息 struct Tick { uint128 liquidityGross; // 总流动性(绝对值) int128 liquidityNet; // 净流动性(带方向) uint256 feeGrowthOutside0X128; // 手续费累积(token0) uint256 feeGrowthOutside1X128; // 手续费累积(token1) // ... 其他字段 } // Position 信息 struct Position { uint128 liquidity; // 流动性数量 uint256 feeGrowthInside0LastX128; // 上次手续费状态 uint256 feeGrowthInside1LastX128; uint128 tokensOwed0; // 待领取手续费 uint128 tokensOwed1; }
v3-periphery(外围合约)
NonfungiblePositionManager.sol(用户主要交互的合约)
contract NonfungiblePositionManager is ERC721 { // 添加流动性(铸造 NFT) function mint(MintParams calldata params) external payable returns ( uint256 tokenId, uint128 liquidity, uint256 amount0, uint256 amount1 ); // 增加流动性 function increaseLiquidity(IncreaseLiquidityParams calldata params) external payable returns (uint128, uint256, uint256); // 减少流动性 function decreaseLiquidity(DecreaseLiquidityParams calldata params) external payable returns (uint256, uint256); // 收取手续费 function collect(CollectParams calldata params) external payable returns (uint256, uint256); // 销毁仓位 function burn(uint256 tokenId) external payable; }
SwapRouter02.sol(交换路由)
contract SwapRouter02 { // 单跳交换(指定输入) function exactInputSingle(ExactInputSingleParams calldata params) external payable returns (uint256 amountOut); // 多跳交换(指定输入) function exactInput(ExactInputParams calldata params) external payable returns (uint256 amountOut); // 单跳交换(指定输出) function exactOutputSingle(ExactOutputSingleParams calldata params) external payable returns (uint256 amountIn); // 多跳交换(指定输出) function exactOutput(ExactOutputParams calldata params) external payable returns (uint256 amountIn); }
用户交互流程
流程 1:添加流动性
User ↓ (调用 mint) NonfungiblePositionManager ↓ (调用 mint) UniswapV3Pool ↓ (更新状态) • 更新 position 数据 • 更新 tick 数据 • 更新 liquidity ↓ (回调) NonfungiblePositionManager ↓ (转账代币) Pool 接收代币 ↓ (返回) User 获得 NFT (tokenId)
流程 2:交换(Swap)
User ↓ (调用 exactInputSingle) SwapRouter02 ↓ (调用 swap) UniswapV3Pool ↓ (计算) • 遍历 tick,计算输出 • 更新 sqrtPriceX96 和 tick • 累积手续费 ↓ (回调) SwapRouter02 ↓ (转账输入代币) Pool 接收输入代币 ↓ (转账输出代币) User 接收输出代币
流程 3:收取手续费
User ↓ (调用 collect) NonfungiblePositionManager ↓ (调用 burn 0 流动性) UniswapV3Pool ↓ (更新手续费) • 计算 feeGrowthInside • 计算应得手续费 • 更新 position.tokensOwed ↓ (调用 collect) Pool 转账手续费 ↓ (返回) User 接收手续费
Gas 优化技巧
V3 合约使用了大量 Gas 优化技巧:
-
位运算代替算术运算
// 除以 2^96: 用右移代替除法 price = (sqrtPriceX96 * sqrtPriceX96) >> 192; // 而不是 / (2**192) -
Tick Bitmap 加速查找:用 bitmap 快速找到下一个初始化的 tick,避免遍历所有 tick
-
只存储非零 tick:只在 tick 有流动性时才初始化,大幅减少存储槽使用
-
使用 unchecked 块:明确不会溢出的运算,跳过检查节省 gas
-
批量更新状态:在函数结束时一次性更新所有状态变量,减少 SSTORE 操作次数
总结
核心要点回顾
1. V3 诞生的动机
- V2 的致命问题:资金利用率极低(大部分流动性永远不会被使用)
- V3 的解决方案:集中流动性(Concentrated Liquidity)
- 核心效果:资金效率提升 4-200 倍
2. 架构层面的根本转变
V2 的设计:储备量 → 计算 → 流动性 , 价格
V3 的设计:流动性 , 价格 → 计算 → 储备量
这个转变使得多个价格区间的流动性叠加成为可能。
3. Tick 机制:价格的离散化
- 公式:
- 每个 tick 代表约 0.01% 的价格变化
- 用整数 tick 表示连续的价格空间
- sqrtPriceX96 优化: 的 Q64.96 定点数表示
4. 储备量计算的数学公式
基础公式:
价格区间公式:
三种特殊情况:
- 价格在区间内:持有 和
- 价格在区间上方:只持有 (全部换成 token1)
- 价格在区间下方:只持有 (全部换成 token0)
反向计算(从代币数量求流动性):
5. 合约架构
核心合约(v3-core):
- UniswapV3Factory:创建池子
- UniswapV3Pool:执行核心逻辑(swap, mint, burn)
外围合约(v3-periphery):
- NonfungiblePositionManager:管理 NFT 仓位
- SwapRouter02:简化交换操作
V3 的权衡取舍
| 维度 | V2 | V3 |
|---|---|---|
| 资金效率 | 低(均匀分布) | 高(集中 4-200 倍) |
| 管理复杂度 | 简单(被动) | 复杂(主动管理) |
| LP Token | ERC20(可互换) | ERC721(NFT,不可互换) |
| 手续费档位 | 单一(0.3%) | 多档(0.01%-1%) |
| Gas 成本 | 低 | 中等(1.5-2 倍) |
| 适用场景 | 被动投资者 | 专业做市商、量化团队 |
附录
官方资源:
社区资源:
合约地址(以太坊主网)
UniswapV3Factory: 0x1F98431c8aD98523631AE4a59f267346ea31F984 SwapRouter02: 0x68b3465833fb72A70ecDF485E0e4C7bD8665Fc45 NonfungiblePositionManager: 0xC36442b4a4522E871399CD717aBDD847Ab11FE88
作者:加密鲸拓
版权:此文章版权归 加密鲸拓 所有,如有转载,请注明出处!